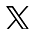Sve informacije o propisu nađite OVDE.

PRAVILNIK O PROGRAMU ZAVRŠNOG ISPITA U OSNOVNOM OBRAZOVANJU I VASPITANJU

("Sl. glasnik RS - Prosvetni glasnik", br. 1/2011, 1/2012, 1/2014, 12/2014, 2/2018, 3/2021, 14/2022, 4/2023 i 5/2023 - ispr.)

« Prethodna strana

Sledeća strana »

Vzdelávacie štandardy pre koniec povinného vzdelávania z matematiky s úlohami

МА.1.1.1. Žiak vie prečítať a zapísať rôzne druhy čísel (prirodzené, celé, racionálne).

Úloha

Pospájaj čiarami rovnaké čísla tak, ako je začaté:

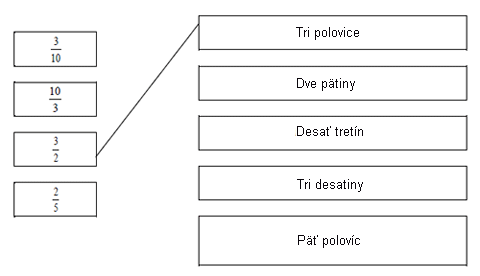
Riešenie

МА.1.1.2. Žiak vie previesť desatinný zápis čísla na zlomok a opačne.

Úloha

Ktoré z ponúknutých čísel sa rovná číslu 0,3?

Zakrúžkuj písmeno pred správnou odpoveďou.

a)	10
a)	3

b)	3
b)	10

c)	1
c)	3

d)	3
d)	1

Riešenie

b)	3
b)	10

МА.1.1.3. Žiak vie usporiadať podľa veľkosti čísla v tom istom zápise pričom použije obrázok, ak je to potrebné.

Úloha

Dané sú čísla:

-3,1

-12,2

0,03

0,3

а) Najmenšie z týchto čísel je:

b) Najväčšie z týchto čísel je:

Riešenie

а) Najmenšie z týchto čísel je:	-12,2

b) Najväčšie z týchto čísel je:	0,3

МА.1.1.4. Žiak vie vykonať jednu základnú matematickú operáciu s číslami toho istého zápisu pomocou obrázka, ak je to potrebné (v prípade sčítania a odčítania zlomkov iba zlomky s rovnakými menovateľmi); počíta, napríklad 1/5 z n, kde je n dané prirodzené číslo.

Úloha

Vypočítaj a napíš zodpovedajúci výsledok:

a) - 6 : 2 = ________

b) - 6 - 2 = ________

c) - 6 ∙ 2 = ________

d) - 6 + 2 = ________

Riešenie

a) - 6 : 2 = −3

b) - 6 - 2 = −8

c) - 6 ∙ 2 = −12

d) - 6 + 2 = −4

МА.1.1.5. Žiak vie deliť jednociferným číslom zo zvyškom a vie, kedy je jedno číslo deliteľné s druhým.

Úloha

Vyplň nasledujúcu tabuľku tak, ako je začaté:

delenec	deliteľ	zvyšok
21376	10	6
123	2
237	3
128	5

Riešenie

delenec	deliteľ	zvyšok
21376	10	6
123	2	1
237	3	0
128	5	3

МА.1.1.6. Žiak vie použiť celé čísla a jednoduché výrazy s nimi pomocou vizuálnych predstáv.

Úloha

Janka má dnes narodeniny a hovorí: "O tri roky budem mať 18 rokov". Koľko rokov má dnes Janka?
Zakrúžkuj písmeno pred správnou odpoveďou.

а) 12

b) 15

c) 18

d) 21

Riešenie

b) 15

МА.1.2.2. Žiak vykonáva formálne operácie ktoré sú redukované a závisia od interpretácie; vie vypočítať mocninu daného čísla, vie základné operácie s mocninami.

Úloha

Zakrúžkuj písmeno pred správnou odpoveďou.
Súčin 210×22 sa rovná:

а) 25

b) 28

c) 212

d) 220

Riešenie

c) 212

Úloha

Zakrúžkuj písmeno pred správnou odpoveďou.
Hodnota mocniny 0,32 је:

а) 0,06

b) 0,6

c) 0,09

d) 0,9

Riešenie

c) 0,09

МА.1.2.1. Žiak vykonáva formálne operácie ktoré sú redukované a závisia od interpretácie; vie riešiť lineárne rovnice, v ktorých je neznámy iba jeden člen

Úloha

Ktoré číslo je riešenie rovnice	x	+2 = 8 ?
	2

Zakrúžkuj písmeno pred správnou odpoveďou.

а) 5

b) 6

c) 12

d) 20

Riešenie

c) 12

МА.1.2.3. Žiak vykonáva formálne operácie ktoré sú redukované a závisia od interpretácie; vie sčítať, odčítať a násobiť jednočleny.

Úloha

Zjednoduš nasledujúce výrazy:

5a3 + 7a3 = _______

9x2 - 4x2 = _______

2b ∙ 3b2 = _______

Riešenie

5a3 + 7a3 = 12a3

9x2 - 4x2 = 5x2

2b ∙ 3b2 = 6b3

МА.1.2.4. Žiak vykonáva formálne operácie ktoré sú redukované a závisia od interpretácie; vie určiť hodnotu funkcie danú tabuľkou alebo vzorcom.

Úloha

Funkcia je daná vzorcom y = 2x + 1. Urči zodpovedajúce hodnoty premenných x a y a vyplň tabuľku.

x	0		4
y		5

Riešenie

x	0	2	4
y	1	5	9

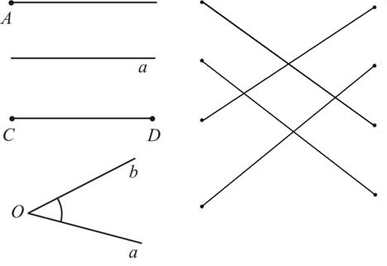
МА.1.3.1. Žiak pozná pojmy: úsečka, polpriamka, priamka, rovina a uhol (všíma si ich modely v reálnych situáciách a dokáže ich narysovať použijúc pomôcky - pravítko, trojuholník a kružidlo; rozlišuje niektoré druhy uhlov a rovnobežné a kolmé priamky).

Úloha

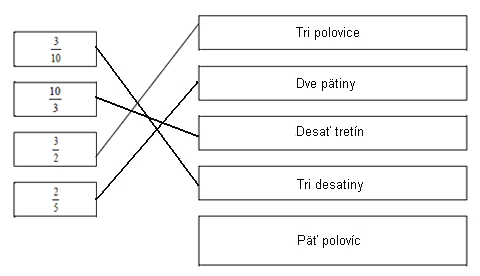
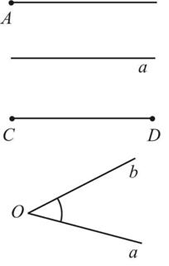
Spoj útvar na obrázku so zodpovedajúcim pojmom (názvom).

	•	• úsečka

	•	• uhol


	•	• polpriamka



	•	• priamka

Riešenie

	úsečka

	uhol


	polpriamka



	priamka

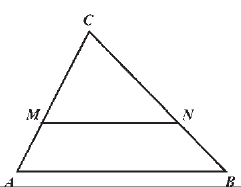
МА.1.3.2. Žiak pozná pojmy: trojuholník, štvoruholník, štvorec a obdĺžnik (všíma si ich modely v reálnych situáciách a dokáže ich narysovať pomocou pravítka, trojuholníka a kružidla; žiak rozlišuje základné druhy trojuholníkov, pozná základné prvky trojuholníka a vie vypočítať obvod a plošný obsah trojuholníka, štvorca a obdĺžnika na základe údajov, ktoré sú priamo dané v úlohe; vie použiť Pytagorovu vetu na výpočet neznámej strany pravouhlého trojuholníka).

Úloha

Akú veľkosť podlahy prikrýva koberec dĺžky 3,5 m a šírky 2 m?

Zakrúžkuj písmeno pred správnou odpoveďou:

а) 11 m2

b) 7 m2

c) 5,5 m2

d) 3,5 m2

Riešenie

b) 7 m2

Úloha

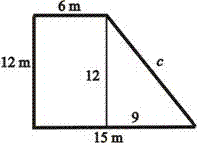
Vypočítaj preponu pravouhlého trojuholníka, ktorý je na obrázku.

c = _____cm

Riešenie

c = 10 cm

МА.1.3.3. Žiak pozná pojmy: kruh, kružnica (vie vyčleniť ich základné prvky, všíma si ich modely v reálnych situáciách a vie ich narysovať pomocou kružidla a pravítka, vie vypočítať obvod a obsah kruhu, keď je daný polomer).

Úloha

Aký je obvod kruhu ktorého polomer je 7 cm?

Zakrúžkuj písmeno pred správnou odpoveďou.

а) 14 cm

b) 49 cm

c) 14p cm

d) 49p cm

Riešenie

c) 14p cm

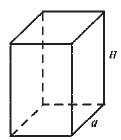
МА.1.3.4. Žiak pozná pojmy: kocka a kváder (všíma si ich modely v reálnych situáciách, pozná ich základné prvky a vie vypočítať ich povrch a objem).

Úloha

Hrana podstavy pravidelného štvorbokého hranola je 6 cm, a výška hranola je 10 cm. Aký je povrch daného hranola?

Povrch hranola je ___________ cm2.

Riešenie

P = 2 ∙ 36 cm2 + 4 ∙ 60 cm2 = 312 cm2

Povrch hranola je 312 cm2.

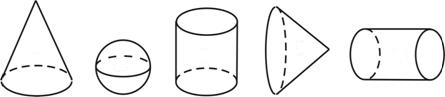
МА.1.3.5. Žiak pozná pojmy: kužeľ, valec, guľa (všíma si ich modely v reálnych situáciách, pozná ich základné prvky).

Úloha

Na každý valec napíš číslo 1, na každý kužeľ číslo 2, a na každú guľu číslo 3.

Riešenie

МА.1.3.6. Žiak intuitívne chápe pojem zhodných útvarov (jeden útvar premiestniť, aby sa kryl s druhým).

Úloha

Ktorý útvar na obrázku je zhodný s útvarom A?

Zakrúžkuj písmeno nad správnou odpoveďou.

Riešenie

Úloha

Daný je útvar F. Vyfarbi čo je potrebné, aby útvar G bol zhodný (aby sa mohol kryť) s útvarom F.



			F



			G

Riešenie



			G

МА.1.4.1. Žiak vie použiť zodpovedajúce jednotky pre meranie dĺžky, plochy, objemu, hmotnosti, času a uhlov.

Úloha

Do prázdneho políčka v tabuľky napíš zodpovedajúcu mernú jednotku.

	Merné číslo	Merná jednotka
Plošný obsah jednej učebne	50
Vzdialenosť medzi Belehradom a Nišom	220
Hmotnosť jedného jablka	120
Cestovanie lietadlom z Belehradu do Atén trvá	2

Riešenie

	Merné číslo	Merná jednotka
Plošný obsah jednej učebne	50	m2
Vzdialenosť medzi Belehradom a Nišom	220	km
Hmotnosť jedného jablka	120	g
Cestovanie lietadlom z Belehradu do Atén trvá	2	hodina alebo h

МА.1.4.2. Žiak vie premeniť väčšie jednotky dĺžky, hmotnosti a času, na menšie.

Úloha

Ktoré časové obdobie je najdlhšie?

Zakrúžkuj písmeno pred správnou odpoveďou.

а) tri mesiace

b) 100 dní

c) 10 týždňov

d) štvrť roka

Riešenie

b) 100 dní

МА.1.4.3. Žiak vie použiť rôzne apoeny peňazí.

Úloha

Ak 3 dvestodinárové bankovky zameníš 50-dinárovými bankovkami, koľko bankoviek dostaneš?

Dostanem ______ bankoviek po 50 dinárov.

Riešenie

Dostanem 12 bankoviek po 50 dinárov.

МА.1.4.4. Žiak si vie zvoliť pri meraní zodpovedajúcu mernú jednotku; zaokrúhliť veličiny vyjadrené danou mierou.

Úloha

Do prázdneho políčka vpíš zodpovedajúcu mernú jednotku: km, cm, l, kg alebo g.

	Merné číslo	Merná jednotka
Množstvo benzínu v nádrži automobilu	50
Vzdialenosť medzi Belehradom a Kruševcom i Novog Sada	200
Hmotnosť jednej hrušky	120
Priemer tenisovej loptičky	8
Hmotnosť jedného psa	12

Riešenie

	Merné číslo	Merná jednotka
Množstvo benzínu v nádrži automobilu	50	l
Vzdialenosť medzi Belehradom a Kruševcom i Novog Sada	200	km
Hmotnosť jednej hrušky	120	g
Priemer tenisovej loptičky	8	cm
Hmotnosť jedného psa	12	kg

МА.1.5.1. Žiak vie vyjadrovať polohu objektov zoraďujúc ich do riadkov a stĺpcov; určiť polohu bodu v prvom kvadrante súradnicovej sústavy ak sú dané súradnice, a opačne.

Úloha

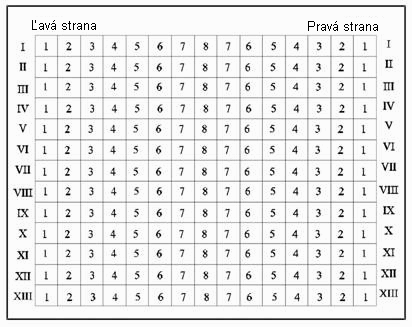
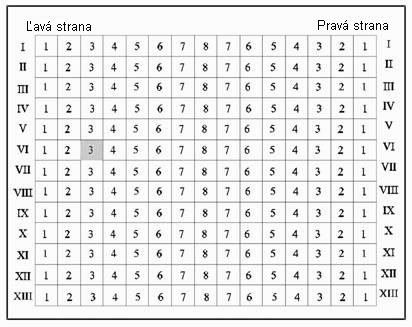
Na obrázku je znázornený plán kina ODEON. Marek si kúpil lístok v šiestom rade na ľavej strane, sedisko číslo 3.
Vyfarbi Marekovo sedisko.

Riešenie

МА.1.5.2. Žiak vie prečítať a pochopiť údaje z grafikonu, diagramu alebo z tabuľky, a určiť minimum a maximum závislej veličiny.

Úloha

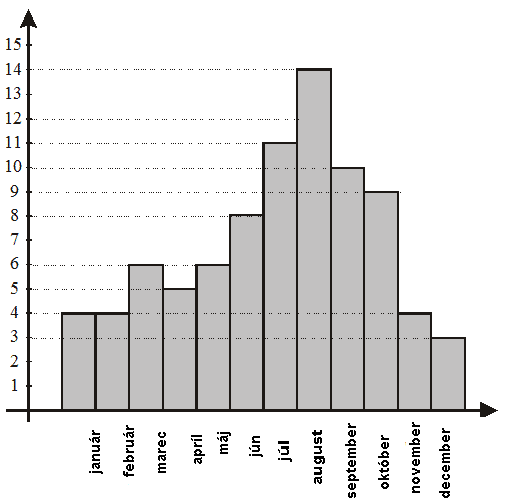
Počet slnečných dní v roku, podľa mesiacov, daný je diagramom.

a) Najmenej slnečných dní v roku bolo v ___________

b) Najviacej slnečných dní v roku bolo v ___________

Riešenie

a) Najmenej slnečných dní v roku bolo v decembri.

b) Najviacej slnečných dní v roku bolo v auguste.

МА.1.5.3. Žiak vie údaje z tabuľky znázorniť grafikonom a opačne.

Úloha

Použi tabuľku úspechu žiakov

Úspech žiakov na písomnej práci
známka	počet žiakov
5	3
4	6
3	12
2	7

adokonči započatý grafikon.

Riešenie

МА.1.5.4. Žiak vie určiť zadané percento nejakej veličiny.

Úloha

Milina sa rozhodla, že si kúpi tenisky ktoré stoja 4 000 dinárov. Pri kúpe dostala od predavača zľavu 10%. Koľko dinárov vynáša zľava ktorú Milina dostala?

Milina dostala zľavu ______ dinárov.

Riešenie

Milina dostala zľavu 400 dinárov.

МА.2.1.1. Žiak vie usporiadať podľa veľkosti čísla zapísané v rôznych tvaroch.

Úloha

Dané sú nasledujúce čísla

-	1		0,2		- 1,2	1	1	.
	2						2

Ktoré z daných čísel je najmenšie, a ktoré najväčšie?

Najmenšie číslo je ________, а najväčšie číslo je _______.

Riešenie

Najmenšie číslo je -1,2, а najväčšie číslo je	1	1	.
		2

МА.2.1.2. Žiak vie určiť opačné číslo, recipročnú (prevrátenú) hodnotu a absolútnu hodnotu čísla; vypočítať hodnotu jednoduchého výrazu a viacerými matematickými operáciami rôznej priority, vrátane oslobádzania od zátvoriek, s číslami rovnakého zápisu.

Úloha

Vypočítaj:

a)		=

b)	3,2 ∙ (4,3+5,7) =

Riešenie

a)		= 1

b)	3,2 ∙ (4,3+5,7) = 32

Úloha

Doplň nasledujúcu tabuľku:

Číslo x

	5
	2

Prevrátená hodnota čísla x

	2
	5

-1

Číslo opačné číslu x

-	5
	2

Riešenie

Číslo x

	5
	2

- 2

	1
	5

- 1 alebo	1
	-1

Prevrátená hodnota čísla x

	2
	5

-	1
	2


5 alebo	1
5 alebo	1
	5

- 1

Číslo opačné číslu x

-	5
	2

-	1
	5

МА.2.1.3. Žiak vie uplatniť základné pravidlá deliteľnosti číslami 2, 3, 5, 9 a dekadickými jednotkami.

Úloha

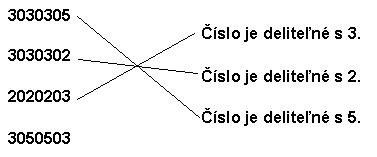
Pospájaj dané čísla so zodpovedajúcimi vetami:

3030305
		Číslo je deliteľné s 3.
3030302
		Číslo je deliteľné s 2.
2020203
		Číslo je deliteľné s 5.
3050503

Riešenie

МА.2.1.4. Žiak vie použiť čísla a číselné výrazy v jednoduchých reálnych situáciách.

Úloha

Za 25 písaniek je zaplatené 750 dinárov. Písanka je o 20 dinárov drahšia ako ceruzka. Koľko sa za tie peniaze mohlo kúpiť ceruziek?
Napíš celý postup.

Za 750 dinárov sa mohlo kúpiť ________ ceruziek.

Riešenie

750 : 25 = 30
Cena písanky je 30 dinárov.
Cena ceruzky је 30 - 20 = 10 dinárov
750 : 10 = 75

Za 750 dinárov sa mohlo kúpiť 75 ceruziek.

МА.2.2.1. Žiak vo vykonávaní matematických operácií dosiahol slušnú úroveň; vie riešiť lineárne rovnice a sústavy lineárnych rovníc s dvoma neznámymi.

Úloha

Zakrúžkuj písmeno pred správnou odpoveďou.
Daná je rovnica . Jej riešenie sa nachádza medzi číslami

a) -20 a -10

b) -10 a 10

c) 10 a 20

d) 20 a 30

Riešenie

c) 10 a 20

МА.2.2.2. Žiak vo vykonávaní matematických operácií dosiahol slušnú úroveň; vie operácie s mocninami a vie čo je druhá odmocnina.

Úloha

Vedľa správneho tvrdenia zakrúžkuj slovo SPRÁVNE, a vedľa nesprávneho tvrdenia slovo NESPRÁVNE.

54∙ 53 = 512	SPRÁVNE	NESPRÁVNE
(23)4 = (24)3	SPRÁVNE	NESPRÁVNE
35 : 34 = 3	SPRÁVNE	NESPRÁVNE
	SPRÁVNE	NESPRÁVNE

Riešenie

54∙ 53 = 512	SPRÁVNE
(23)4 = (24)3		NESPRÁVNE
35 : 34 = 3		NESPRÁVNE
	SPRÁVNE

МА.2.2.3. Žiak vo vykonávaní matematických operácií dosiahol slušnú úroveň; vie sčitovať a odčitovať mnohočleny, vie vynásobiť dva dvojčleny a určiť druhú mocninu dvojčlena.

Úloha

Druhá mocnina dvojčlena	(	1	m - n)2 je:
		2

а)	1	m2 + 2mn + n2
а)	2	m2 + 2mn + n2

b)	1	m2 - mn + n2
b)	4	m2 - mn + n2

c)	1	m2 - mn + n2
c)	2	m2 - mn + n2

d)	1	m2 - n2
d)	4	m2 - n2

Riešenie

b)		1	m2 - mn + n2
		4

МА.2.2.4. Žiak vo vykonávaní matematických operácií dosiahol slušnú úroveň; vie zistiť závislosť medzi premennými, pozná funkciu y = ax a vie graficky interpretovať jej vlastnosti; na tie vlastnosti nadviazať pojem priamej úmernosti a určiť neznámy člen úmery.

Úloha

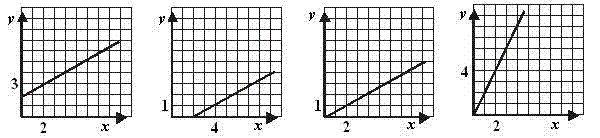
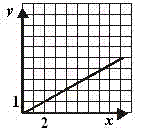
Na jednom z daných výkresov je znázornená závislosť medzi množstvom olova (x) a zinku (y) v zliatine, ktorá obsahuje olovo a zinok v pomere 2 : 1.

Zakrúžkuj písmeno nad obrázkom, na ktorom je znázornená závislosť medzi olovom a zinkom v tej zliatine.

Riešenie

Úloha

Za 8 m látky treba zaplatiť 2 400 dinárov.

a) Koľko stojí 12 m takej istej látky?

b) Koľko metrov takej istej látky sa môže kúpiť za 750 dinárov?

а) 12 m látky stojí _______ dinárov.

b) Za 750 dinárov sa môže kúpiť _________ metrov látky.

Riešenie

а) 12 m látky stojí 3600 dinárov.

b) Za 750 dinárov sa môže kúpiť 2,5 metrov látky.

МА.2.2.5. Žiak vo vykonávaní matematických operácií dosiahol slušnú úroveň; vie použiť rovnice v jednoduchých slovných úlohách.

Úloha

Keď Peter strovil tretinu svojich úspor na zaplatenie kreditu pre mobilný telefón, zostalo mu ešte 800 dinárov. Aké boli Petrove úspory?

Petrove úspory boli _______ dinárov.

Riešenie

Petrove úspory boli 1200 dinárov.

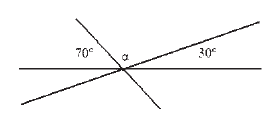
МА.2.3.1. Žiak vie určiť výplnkové a doplnkové uhly, susedné (vedľajšie) a vrcholové uhly; vie počítať s nimi ak sú vyjadrené celými stupňami.

Úloha

Urči veľkosť uhla α, ktorý je na obrázku.

α = ______________

Riešenie

α = 80°

МА.2.3.2. Žiak vie určiť vzťah strán a uhlov trojuholníka, súčet uhlov trojuholníka a štvoruholníka a pri riešovaní úloh uplatniť Pytagorovu vetu.

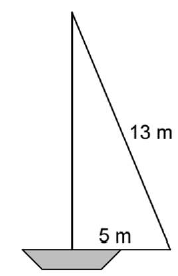
Úloha

Na obrázku je plachetnica. Aký je plošný obsah plachty znázornenej na obrázku?

Napíš celý postup.

Plošný obsah plachty je ________ m2.

Riešenie

Ak je výška stožiara x, potom је x2 = 132 - 52 = 169 · 25 = 144.

Výška stožiara je 12 m. Plošný obsah plachty je P =	1	12 · 5 = 30 m2
	2

Plošný obsah plachty je 30 m2.

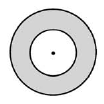
МА.2.3.3. Žiak vie použiť vzorce pre obvod a obsah kruhu a medzikružia.

Úloha

Plošný obsah menšieho kruhu je 9p cm2. Plošný obsah medzikružia је 16p cm2.

Vypočítaj polomer väčšieho kruhu.

Polomer väčšieho kruhu je ____ cm.

Riešenie

Pvk = (9p + 16p ) cm2 = 25p cm2
r2p = 25p cm2
r = 5 cm

Polomer väčšieho kruhu је 5 cm.

МА.2.3.5. Žiak vie vypočítať povrch a objem valca, kužeľa a gule, keď sú potrebné prvky priamo dané v úlohe.

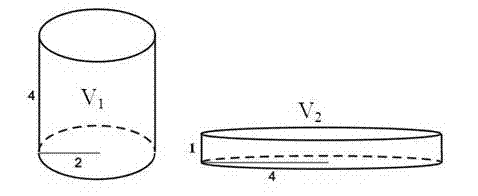
Úloha

Na obrázku sú dva valce ktorých objemy sú V1 a V2.

Zakrúžkuj písmeno pred správnou odpoveďou.

а) V1 > V2

b) V1 < V2

c) V1 = V2

Riešenie

c) V1 = V2

МА.2.3.6. Žiak vie spozorovať osovo súmerné útvary a určiť os súmernosti; použiť zhodnosť a jej spätosť s charakteristickými vlastnosťami útvarov (napr. rovnobežnosť a zhodnosť strán rovnobežníka).

Úloha

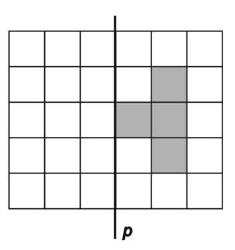
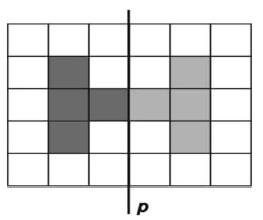
Vyfarbi políčka na obrázku, tak aby sa dostal osovo súmerný útvar vzhľadom na priamku p.

Riešenie

МА.2.4.1. Žiak vie porovnať veličiny, ktoré sú vyjadrené rôznymi jednotkami na meranie dĺžky a hmotnosti.

Úloha

Učiteľka na tabuľu napísala hmotnosť štyroch predmetov.
Zakrúžkuj písmeno pod predmetom, ktorý je najťažší.

1kg 20g		1,2kg		1022g		1,002kg
a)		b)		c)		d)

Riešenie

1,2kg
b)

Úloha

V predajni majú tri očistené kuriatká, ktorých hmotnosť je 1340 g, 1,35 kg, respektíve 1 kg 290 g.

Usporiadaj tie hmotnosti podľa veľkosti, od najväčšej po najmenšiu.

Odpoveď: ________ > _________ > ________

Riešenie

1,35 kg > 1340 g > 1kg 290 g

МА.2.4.2. Žiak vie premeniť hodnoty jednej valuty do druhej pomocou zodpovedajúcej úmery.

Úloha

Maja novoročné sviatky strávila v Taliansku. Cena pobytu s cestou bola 200 eúr.
Akú sumu Maja zaplatila v dinároch, ak v deň platenia 1 euro malo hodnotu 105 dinárov?

Maja zaplatila _____________ dinárov.

Riešenie

Maja zaplatila 21 000 dinárov.

Úloha

Ak jedna nórska koruna má hodnotu 12,50 dinárov a jedno euro 105 dinárov, akú hodnotu má 10 eúr v nórskych korunách?
Napíš celý postup.

10 eúr má hodnotu______ nórskych korún.

Riešenie

10 eúr je 105 × 10 = 1050 dinárov. 1050 : 12,5 = 84

10 eúr má hodnotu 84 nórske koruny.

МА.2.4.3. Žiak vie danú veličinu vyjadriť približnou hodnotou.

Úloha

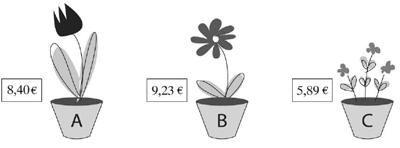
Kvetinár má ceny kvetov z dovozu zaokrúhliť na najbližšie celé číslo. Vpíš nové ceny do danej tabuľky.

Rastlina	A	B	C
Nová cena

Riešenie

Rastlina	A	B	C
Nová cena	8	9	6

МА.2.5.1. Žiak pozná súradnicovú sústavu (vie určiť súradnice bodov, osovo alebo stredovo súmerných atď.).

Úloha

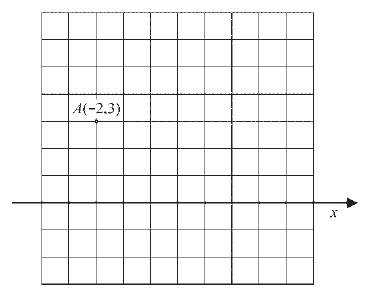
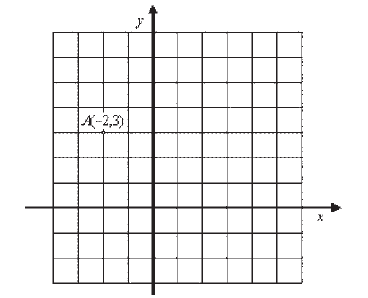
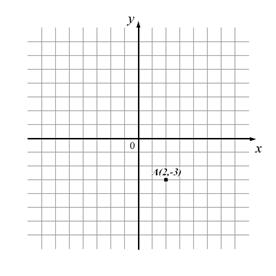
Na základe daných súradníc bodu A, narysuj os y Dékartovej pravouhlej súradnicovej sústavy.

Riešenie

МА.2.5.2. Žiak vie čítať jednoduché diagramy a tabuľky, a na základe nich spracovať údaje podľa jedného kritéria (napr. určiť aritmetický stred pre danú množinu údajov; porovnať hodnoty výrazu so strednou hodnotou).

Úloha

V danej tabuľky je vzdialenosť medzi jednotlivými mestami vyjadrená v kilometroch.

Belehrad
Čačak	144
Kragujevac	120	87
Nikšić	536	395	482
Niš	239	186	143	576
Nový Sad	81	225	219	616	314
Zreňanin	80	224	200	616	319	50
Vzdialenosť v kilometroch	Belehrad	Čačak	Kragujevac	Nikšić	Niš	Nový Sad	Zreňanin

Na základe údajov, ktoré sú dané v tabuľke, doplň nasledujúce vety tak, aby boli správne.

а) Vzdialenosť medzi Čačkom a Nikšićom je _______ kilometrov.

b) Vzdialenosť medzi Nikšićom a ______________ је rovnaká ako aj

vzdialenosť medzi Nikšićom a ________________ .

Riešenie

а) Vzdialenosť medzi Čačkom a Nikšićom je 395 kilometrov.

b) Vzdialenosť medzi Nikšićom a Novým Sadom је rovnaká ako aj

vzdialenosť medzi Nikšićom a Zreňaninom.

МА.2.5.3. Žiak vie spracovať zozbierané údaje a znázorniť ich tabuľkou alebo graficky; vie určiť medián stredných hodnôt.

Úloha

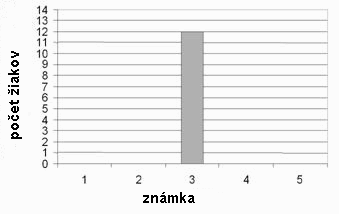
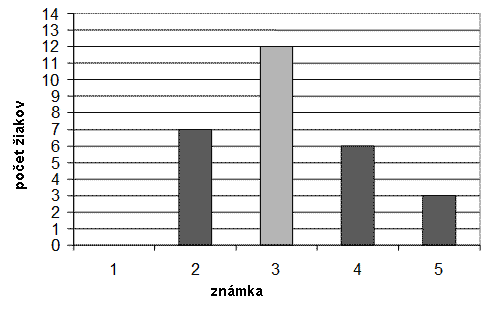
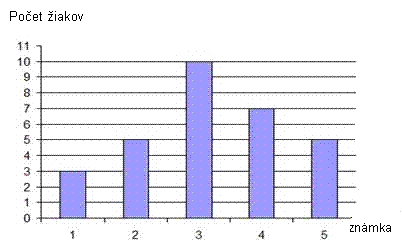
Diagramom na obrázku znázornený je úspech žiakov jedného oddelenia na teste z matematiky.

а) Doplň tabuľku, ktorá zodpovedá danému diagramu, tak ako je začaté:

Úspech žiakov na teste z matematiky
známka	počet žiakov
5
4
3
2
1	3

b) Vypočítaj strednú známku na teste z matematiky.

Stredná známka na teste z matematiky je ________

Riešenie

а)

Úspech žiakov na teste z matematiky
známka	počet žiakov
5	5
4	7
3	10
2	5
1	3

b) Stredná známka na teste z matematiky je 3,2.

МА.3.1.2. Žiak vie vhodne používať pojem deliteľnosti v problémových situáciách.

Úloha

Napíš tri čísla piatej tisícky, ktorých číslica desiatok je 2, a ktoré sú deliteľné číslom 9.

Sú to čísla _______, ________, ________.

Riešenie

Napísané hociktoré tri čísla z množiny {4023, 4122, 4221, 4320, 4329, 4428, 4527, 4626, 4725, 4824, 4923}.

МА.3.1.3. Žiak vie použiť čísla a číselné výrazy v reálnych situáciách.

Úloha

Kvetinárka robí a predáva kytice. V každej kytici sú 4 ruže a 3 margaréty. Ak kvetinárka na každej predanej ruži zarobí 35 dinárov, na každej predanej margaréte 25 dinárov a na robení kytice 60 dinárov, koľko najmenej kytíc má predať, aby zarobila viac ako 1500 dinárov?
Napíš celý postup.

Kvetinárka má predať najmenej _____ kytíc.

Riešenie

Zárobok na jednej kytici: 4 · 35 + 3 · 25+ 60 = 140 + 75 + 60 = 275

275 · 5 = 1375, 275 · 6 = 1650 alebo 1500 : 275 = 5,45…

Kvetinárka má predať najmenej 6 kytíc.

МА.3.2.2. Žiak dosiahol vysokú úroveň vo vykonávaní matematických operácií so zdôrazňovaním vlastností ktoré sa uplatňujú; vie uplatniť vlastnosti mocniny a druhej odmocniny.

Úloha

Ak sa vie, že je 322 = 1024, vypočítaj:

а) = ______________

b) = _____________

c) = ______________

Riešenie

a) = 3,2

b) = 320

c) = 0,32

МА.3.2.3. Žiak dosiahol vysokú úroveň vo vykonávaní matematických operácií so zdôrazňovaním vlastností ktoré sa uplatňujú; vie uplatniť vzorce pre rozdiel druhých mocnín (rozdiel štvorcov) a druhú mocninu (štvorec) dvojčlena; algebrické výrazy šikovne transformovať a upraviť na najjednoduchší tvar.

Úloha

Zakrúžkuj písmeno pred správnou odpoveďou.

Mnohočlen (а - 1)(2а + 1) - (а - 6)(а + 6) sa rovná mnohočlenu:

a) а2 − а + 35

b) а2 − а − 37

c) а2 + 35

d) а2 - 37

Riešenie

а) а2 - а + 35

Úloha

Vypočítaj:

а) rozdiel druhých mocnín čísel 7 a 3 : ______________________________

b) druhú mocninu rozdielu čísel 7 a 3 : _____________________________

c) súčet druhých mocnín čísel 7 a 3 : ______________________________

d) druhú mocninu súčtu čísel 7 a 3 : _______________________________

Riešenie

а) 72 - 32 = 49 - 9 = 40

b) (7 − 3)2 = 42 = 16

c) 72 + 32 = 49 + 9 = 58

d) (7 + 3)2 = 102 = 100

МА.3.2.4. Žiak dosiahol vysokú úroveň vo vykonávaní matematických operácií so zdôrazňovaním vlastností ktoré sa uplatňujú; vie rozlíšiť priamoúmerné a nepriamoúmerné veličiny a vyjadriť to zodpovedajúcim zápisom; pozná lineárnu funkciu a vie graficky interpretovať jej vlastnosti.

Úloha

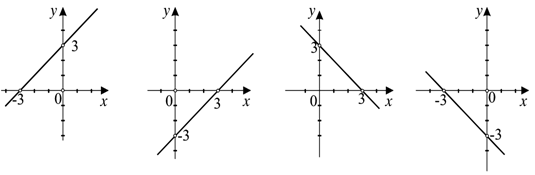
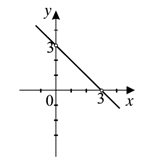
Na ktorom obrázku je znázornený graf funkcie y = −x + 3?
Zakrúžkuj písmeno nad správnou odpoveďou.

а)	b)		c)	d)

Riešenie

Úloha

Deviati priatelia by očistili bazén za štyri dni. Koľký priatelia by im ešte mali pomôcť, aby bazén bol očistený za tri dni?

Bazén bude očistený za tri dni, ak im pomôžu ešte ____ priatelia.

Riešenie

9 : x = 3 : 4 alebo x : 9 = 4 : 3
x = 12
12 - 9 = 3

Bazén bude očistený za tri dni, ak im pomôžu ešte 3 priatelia.

МА.3.2.5. Žiak dosiahol vysokú úroveň vo vykonávaní matematických operácií so zdôrazňovaním vlastností ktoré sa uplatňujú; vie použiť rovnice, nerovnice a sústavy rovníc na riešovanie zložitejších slovných úloh.

Úloha

Kým bola na letovaní, Naďa každému zo svojich 9 priateľov poslala alebo list alebo pohľadnicu. Na pohľadnice kúpila známky po 10 dinárov a na listy známky po 15 dinárov. Koľko listov a koľko pohľadníc Naďa poslala, ak na známky strovila spolu 110 dinárov?
Napíš celý postup.

Naďa poslala _________ listov a _________ pohľadnice.

Riešenie

x - počet listov
y - počet pohľadníc

x + y = 9
10x + 15y = 110

Riešenie sústavy je x = 5 a y = 4, bezohľadu na metódu, ktorou sa sústava rieši.

Naďa poslala 5 listov a 4 pohľadnice.

МА.3.3.1. Žiak vie počítať s uhlami vrátane premieňania jednotiek pre meranie uhlov; donášať uzávery na základe vlastností rovnobežných a kolmých priamok, vrátane uhlov na priečke (transverzále).

Úloha

Ak sú priamky a a b rovnobežné, urči veľkosť uhla a.

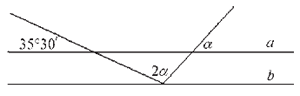Uhol a =____

Riešenie

Uhol a = 48°10΄

МА.3.3.2. Žiak vie uplatniť základné vlastnosti trojuholníka, štvoruholníka, rovnobežníka a lichobežníka, vypočítať ich obvody a obsahy na základe údajov, ktoré nemusia byť dané priamo vo formulácii úlohy; vie ich zostrojiť.

Úloha

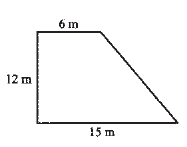
Koľko metrov drôtu je potrebné, aby sa ohradil dvor tvaru pravouhlého lichobežníka ako na obrázku?

Napíš celý postup.

Potrebné je _____ metrov drôtu.

Riešenie

c2 = 122 + 92
c2 = 225
c = 15

O = 12 + 15 +15 + 6
O = 48 m

Potrebné je 48 metrov drôtu.

МА.3.3.3. Žiak vie určiť stredový a obvodový uhol, vypočítať obsah kruhového výseku ako aj dĺžku kruhového oblúka.

Úloha

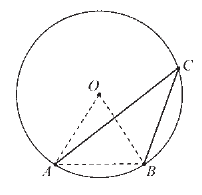
Ak je tetiva AB zhodná s polomerom kruhu, vypočítaj uhol ACB.

ÐABC = ____________

Riešenie

ÐABC = 30°

Úloha

Koľkokrát je obsah kruhového výseku ktorého stredový uhol je 30°, menší od obsahu kruhu?

Menší je ____ krát.

Riešenie

Menší je 12-krát.

МА.3.3.4. Žiak vie vypočítať povrch a objem hranola a ihlana vrátane prípadov, keď potrebné prvky nie sú dané priamo.

Úloha

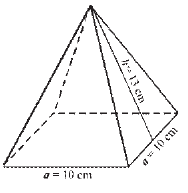
Vypočítaj objem pravidelného štvorbokého ihlana ak je hrana jeho podstavy a = 10 cm, a výška bočnej steny h = 13 cm.

Napíš celý postup.

Objem ihlana je ________ cm3.

Riešenie

H2 = h2 - (	a	)2, H2 = 132 - 52, H2 = 169 - 25, H2 = 144, H = 12 cm
	2

V=	1	B · H , V =	1	a2 · H, V =	1	· 100 · 12 , V = 400 cm3
	3		3		3

Objem ihlana je 400 cm3.

МА.3.3.5. Žiak vie vypočítať povrch a objem valca, kužeľa a gule vrátane prípadov, keď potrebné prvky nie sú dané priamo.

Úloha

Zakrúžkuj písmeno pred správnou odpoveďou.

Pravouhlý trojuholník s odvesnami а = 9 cm, b = 12 cm, sa otáča okolo odvesny b. Plošné obsahy podstavy a plášťa vzniknutého kužeľa sú v pomere:

a) 1 : 1

b) 3 : 4

c) 3 : 5

d) 4 : 5

Riešenie

c) 3 : 5

Úloha

Aký je povrch najväčšej možnej gule ktorá sa vmestí do škatule tvaru kocky s hranou 20 cm?

Povrch gule je ____ cm2.

Riešenie

Povrch gule je 36p cm2.

МА.3.3.6. Žiak vie uplatniť zhodnosť a podobnosť trojuholníkov, a tak navzájom zjednotiť rôzne vlastnosti geometrických útvarov.

Úloha

Úsečka MN je rovnobežná s úsečkou АВ. Ak je MN : AB = 2 : 3, aký je pomer СМ : MА?

Zakrúžkuj písmeno pred správnou odpoveďou.

a) 2 : 1

b) 3 : 1

c) 3 : 2

d) 2 : 3

Riešenie

а) 2 : 1

Úloha

Vedľa správneho tvrdenia zakrúžkuj slovo Správne, a vedľa nesprávneho tvrdenia slovo Nesprávne.

Každé dva rovnostranné trojuholníky sú podobné

Správne

Nesprávne

Riešenie

Každé dva rovnostranné trojuholníky sú podobné		Nesprávne
Každé dva podobné trojuholníky majú rovnaké obvody	Správne
Dva rovnoramenné trojuholníky ktorých uhol pri hlavnom vrchole má veľkosť 36° sú podobné		Nesprávne
Všetky pravouhlé trojuholníky sú podobné	Správne

МА.3.4.2. Žiak vie odhadnúť a zaokrúhliť dané údaje, a počítať s tak získanými približnými hodnotami; vyjadriť hodnotu chyby (napr. menšie ako 1 dinár, 1 cm, 1 g).

Úloha

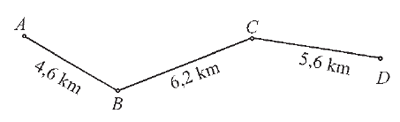
Na nasledujúcej mape je znázornená vzdialenosť medzi mestami A a D.

Mirka a Vierka určovali koľko celých kilometrov je medzi mestami A a D. Mirka určila vzdialenosť medzi mestami A a D tak, že každú z uvedených vzdialeností zaokrúhlila na najbližšie celé číslo a potom ich sčítala. Vierka sčítala vzdialenosti na mape, a získaný výsledok zaokrúhlila na najbližšie celé číslo.

Zakrúžkuj písmeno pred správnou odpoveďou.

a) Mirka dostala väčšie číslo od Vierky.

b) Mirka a Vierka dostali rovnaké čísla.

c) Mirka dostala menšie číslo od Vierky.

Riešenie

a) Mirka dostala väčšie číslo od Vierky.

МА.3.5.1. Žiak vie určiť polohu (súradnice) bodov, ktoré spĺňajú zložitejšie podmienky.

Úloha

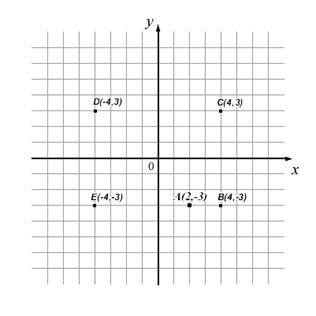
V súradnicovej sústave označ všetky body ktoré sú od osi x rovnako vzdialené ako bod A, a ich vzdialenosť od osi y je dvakrát väčšia ako vzdialenosť bodu A od osi y.

Riešenie

Úloha

V tabuľke sú dané vzdialenosti medzi niektorými mestami v kilometroch.

km	Belehrad	Kragujevac	Niš	Nový Sad	Novi Pazar	Subotica	Zaječar
Belehrad	-	115	239	82	271	178	236
Jagodina	165	42	104	217	196	319	117
Kragujevac	115	-	146	197	160	299	159
Kraljevo	192	54	152	251	106	353	193
Kruševac	192	70	91	274	167	376	132

а) Ktoré mesto je od Belehradu vzdialené 115 km? .......................

b) Ktoré dve mestá sú od seba vzdialené 353 km? ...............................................

c) Ktoré dve mestá sú od seba vzdialené menej ako 50 km? .....................................

d) Koľko miest v danej tabuľke je od Belehradu vzdialené viacej ako 200 km? ........

Riešenie

a) Kragujevac

b) Kraljevo a Subotica

c) Јagodina a Kragujevac

d) tri

МА.3.5.2. Žiak vie vysvetliť diagramy a tabuľky.

МА.3.5.3. Žiak vie zozbierať a spracovať údaje, a samostatne urobiť diagram alebo tabuľku; vie nakresliť graf ktorým znázorní závislosť veličín.

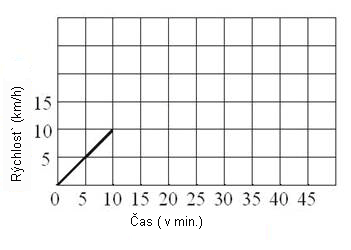
Úloha

Maja jazdila na bicykli 45 minút. Po prvých 10 minútach jazdy dosiahla rýchlosť 10 km/h. Takou rýchlosťou jazdila nasledujúcich 20 minút, a potom začala rovnomerne spomaľovať, kým sa celkom nezastavila. Doplň diagram ktorý znázorňuje Majinu jazdu, tak ako je začaté.

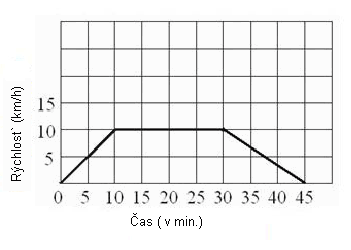
Riešenie

МА.3.5.4. Žiak vie použiť percentové výpočty v zložitých situáciách.

Úloha

Cenu knihy najprv zvýšili o 10%, potom znížili o 10% a teraz vynáša 198 dinárov. Aká bola cena knihy pred zvýšením?

Zakrúžkuj písmeno pred správnou odpoveďou.

a) 198 dinárov

b) 200 dinárov

c) 202 dinárov

d) 196,02 dinárov

Riešenie

b) 200 dinárov

Vzdelávacie štandardy pre koniec povinného vzdelávania z matematiky, ktoré budú preverované neznámymi úlohami

MА.2.3.4. Žiak vie čo je hranol a ihlan (pojem); vie vypočítať ich povrch a objem, keď sú potrebné prvky priamo dané v úlohe.

Úloha

Hrana podstavy pravidelného trojbokého ihlana, ktorého všetky hrany sú rovnako dlhé, je 8 cm. Aký je jeho povrch?
Napíš celý postup.

Povrch ihlana je ___________ cm2

Riešenie

Ps =	a2	Ö 3 = 16Ö 3 cm2
	4

P =	4 · Ps = a2Ö 3 = 64Ö 3 cm2

alebo

P = 4 ·	a2	Ö 3 = a2 Ö 3 = 64Ö 3 cm2
	4

Povrch ihlana je 64 Ö 3 cm2.

МА.2.5.4. Žiak vie použiť percentové výpočty v jednoduchých reálnych situáciách (napríklad, zmena ceny nejakého tovaru o dané percento).

Úloha

Gordana predáva zmrzlinu po cene 60 dinárov. Na každej predanej zmrzline má zárobok 6 dinárov. Aký je jej zárobok na jednej predanej zmrzline vyjadrený v percentách?

Zakrúžkuj písmeno pred správnou odpoveďou.

а) 6 %

b) 1 %

c) 54 %

d) 10 %

Riešenie

d) 10 %

МА.3.1.1. Žiak vie určiť hodnotu zložitejšieho číselného výrazu.

Úloha

Vypočítaj súčin výrazov А a В, ak je a B =.

А = _______ , B = ______ , súčin A · B = _______

Riešenie

A =	3, B =	2	, súčin A · B = 2
		3

МА.3.2.1. Žiak dosiahol vysokú úroveň vo vykonávaní matematických operácií so zdôrazňovaním vlastností ktoré sa uplatňujú; vie postaviť a riešiť lineárne rovnice a nerovnice a sústavy lineárnych rovníc s dvoma neznámymi.

Úloha

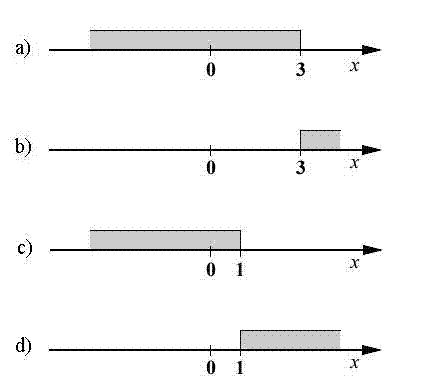
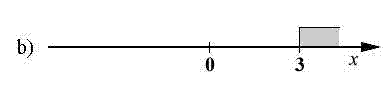
Ktorá množina čísel, znázornená na číselnej osi, je riešenie nerovnice